Molecular Materials for Quantum Technologies
Piligkos Group
My group investigates the suitability of coordination complexes based on lanthanide and transition metal ions for use within quantum information technologies. To this purpose we synthesise new coordination complexes and study their structures and electronic properties by a variety of thermodynamic and spectroscopic techniques, with emphasis on magnetic properties. We are especially interested in coherent and incoherent static and dynamic magnetic properties. We also develop software for the modeling of these.
By synthesising derivatives of such complexes we rationalise how a particular molecular design can optimise the dynamic magnetic properties of our complexes.
Further, we also develop protocols for the transfer of these coordination complexes from the solid state to surfaces via, in general, solution chemistry methods. This is a key step for the integration of molecular magnetic materials in quantum information devices.
Ideas for student projects
In my group we are always on the look for new students who are interested in joining us to perform a research project. Many different types of projects are available in my group, ranging from synthesis of new lanthanide complexes to writing your own computer programs to model the electronic properties of lanthanide complexes.
For most projects, we synthesise new lanthanide or transition metal complexes, study their magnetism through spectroscopies and magnetometry and model the obtained data to determine the electronic structure of these molecular materials. We have a range of measurement techniques available in-house, including luminescence and UV/Vis spectroscopies, magneto-circular dichroism, X-, Q- and L-band electron paramagnetic resonance (EPR) and SQUID magnetometry. The above techniques can all be performed at cryogenic conditions.
In addition, we collaborate with many groups with access to additional measurement techniques such as torque magnetometry, pulse EPR and high-magnetic field electron paramagnetic resonance. From 2023, my group will have access to in-house pulse EPR and Pulse Electron Nucleus Double Resonance (ENDOR) at X- and Q-bands.
Quantum Computers (QCs) are devices that exploit genuine quantum properties of matter, such as superposition states or entanglement, allowing them to outperform today’s best supercomputers (Quantum Advantage) for some specific types of computations. These include prime-number factorisation (the basis of currently used encryption protocols), the management of large databases and the accurate simulation of quantum many-body systems. Attaining Quantum Advantage will change the way in which we process, search and share information, including artificial intelligence (through quantum machine learning), and have a transformative impact on the simulation and development of novel materials and chemicals with applications in energy (magnets, batteries, superconductors), agriculture (more efficient and sustainable fertilizers) or biomedicine and biotechnologies.
In QCs the smallest logical unit is the quantum bit, a two-level quantum system that can assume the states |0> or |1> or any arbitrary linear combination of these, such as: a|1> + b|0>, with a and b being complex numbers. A quantum information register can therefore process information states that are forbidden to a classical one and, in particular, handle all possible outcomes of a given computational problem. This ‘‘quantum parallelism’’ gives a resource that can greatly simplify some computational tasks.
We recently demonstrated that Yb(trensal) is an excellent electronic qubit displaying coherent Rabi oscillations of the electronic spin extending to the microsecond region (paper). Additionally, in collaboration with colleagues at the University of Parma, we showed that Yb(trensal) is a prototypical coupled electronic-qubit−nuclear-qudit (paper) and put forward a proposal to exploit the multilevel structure of the qudit to encode a logical qubit protected against both amplitude or phase shift errors. Here the nuclear qudit encodes the quantum information and the electronic qubit is used as an ancilla to detect errors. Thus, we developed molecular prototypical electronic-qubit-nuclear-qudit coupled systems in which quantum error correction can be intrinsically implemented.
We have also extended the trensal motif and made the complexes functionalizable and ready for surface deposition (paper).
Your project: In your project you will be working on preparing new Ln(trensal) qubits and study their electronic structure, spin-lattice relaxation and coherent magnetic properties.
In classical computers, the basic unit of computation is the bit, which in binary logic can take two values, |0> or |1>. Implementation of classical bits uses as physical support classical systems displaying two well defined states. In Quantum Computers (QCs), the basic unit of computation is the quantum bit or qubit. Its physical implementation is a two-level quantum system that can assume the states |0> or |1> or any arbitrary linear combination of these, such as: a|1> + b|0>, with a and b being complex numbers. This ‘‘quantum parallelism’’, is expected to enormously increase the potential of information processing. Quantum computing operations are performed by logic quantum gates. The simplest of these are single qubit unitary rotations which, starting from a basis state, say |0> or |1>, produce a superposition, such as: a|1> + b|0>. Quantum computing algorithms can be performed as a sequence of single qubit rotations and gate operations performed on two entangled qubits. For example, in binary arithmetic addition modulus two is performed by the controlled-NOT gate that inverts the state of one qubit (target qubit) if, and only if, the other one (control qubit) is, for example, in the |0> state.
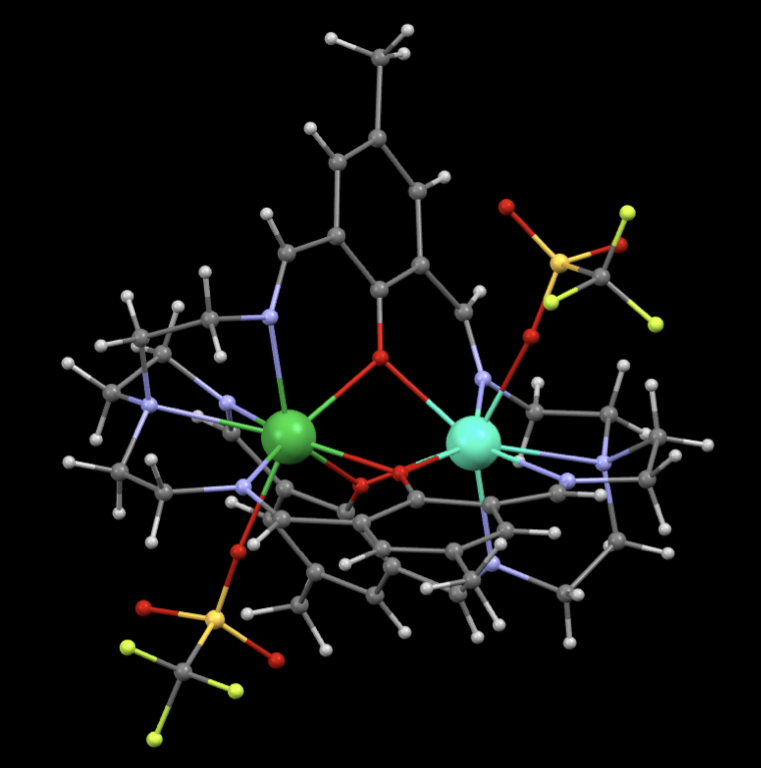
In my group we investigate the potential of heterodinuclear lanthanide complexes to be used as entangled two-qubit quantum gates. Due to the very similar chemistry of the 14 lanthanide ions, heterolanthanide complexes are inherently difficult to synthesise. We recently presented a synthetic procedure to synthesise all dinuclear lanthanide complexes involving Gd-Lu (paper). These complexes are based on the cryptand ligand shown above, which ensures the stability of the complexes, a vital asset for their inclusion in future quantum technology devices.
Your project: You will synthesise new heteronuclear lanthanide complexes based on our established synthetic procedure and study the magnetic properties of these, with emphasis on determining the interaction between the two lanthanide centers and on the coherent magnetic properties of these systems. Additionally, you will be working on extending the choice of lanthanides beyond the late lanthanides (Gd-Lu) to the early lanthanides (Ce-Eu).
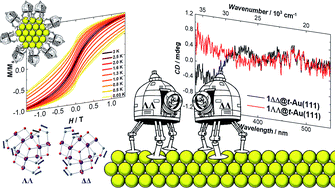
A prerequisite for molecular materials to be used for the realisation of Quantum Information devices is that they need to be placed on a surface (gold, silicon, metal oxides, graphene etc.) in a controlled way. Additionally, they need to be addressable at the single molecule level by external stimuli such as photons or electric fields, which, for example, can be obtained through chiral molecules for the latter. However, it is not obvious that the molecular properties as determined in the solid state or in solution are maintained upon surface deposition. In general a radical modification of these properties is observed after surface deposition.
In 2019 we published studies on a manganese(III) based single-molecule magnet which retains its hysteretic magnetic properties and chirality upon deposition on a gold surface (paper). Recently we have investigated derivatives of the Ln(trensal) complexes which can be functionalised for surface deposition on various surfaces (paper). Additionally, we have investigated chiral versions of the Ln(trensal) complexes.
Your project: You will synthesise new Ln(trensal) derivatives that can be attached to surfaces. You will study the bulk properties of these complexes before and after depositing them on a surface e.g. graphene, and compare these properties to the ones in the bulk.
- Coordination chemistry
- Study of magnetic properties by spectroscopic and thermodynamic techniques
- Modeling Software
- Coherent magnetic properties
- Lanthanide-based magnets
- Electronic structure of transition metals and of lanthanides
- Polynuclear systems
- Lanthanide-based quantum computing devices
cw EPR
Continuous wave Electron paramagnetic resonance (EPR) measurements can be performed on a Bruker Elexsys E500 instrument with an Oxford Cryosystem temperature controller allowing for temperatures in the range 4 - 300 K. Measurements can be performed at L-, X- and Q-band frequencies. The electromagnet of the instrument can generate fields up to 1.7 T.

SQUID
Magnetometry measurements can be performed on a Quantum-Design MPMS-XL SQUID magnetometer. Measurements can be performed at temperatures ranging from 1.8 - 300 K with fields ranging from 0 - 5 T. For AC susceptibility measurements the oscillating magnetic field can be set to 0.1 - 1500 Hz. 
Luminescence spectroscopy

Magnetic Circular Dichroism

Group members
| Name | Title | Phone | |
|---|---|---|---|
| Asger Strandfelt | PhD Fellow | +4535326029 | |
| Lukas Bradley Woodcock | Special Consultant | +4535331567 | |
| Michael David Roy | Postdoc |
